Clinical Application of Gamma Knife Dose Verification Method in Multiple Brain Tumors : Modified Variable Ellipsoid Modeling Technique
Article information
Abstract
Objective
The Leksell Gamma Knife® (LGK) is based on a single-fraction high dose treatment strategy. Therefore, independent verification of the Leksell GammaPlan® (LGP) is important for ensuring patient safety and minimizing the risk of treatment errors. Although several verification techniques have been previously developed and reported, no method has ever been tested statistically on multiple LGK target treatments. The purpose of this study was to perform and to evaluate the accuracy of a verification method (modified variable ellipsoid modeling technique, MVEMT) for multiple target treatments.
Methods
A total of 500 locations in 10 consecutive patients with multiple brain tumor targets were included in this study. We compared the data from an LGP planning system and MVEMT in terms of dose at random points, maximal dose points, and target volumes. All data was analyzed by t-test and the Bland-Altman plot, which are statistical methods used to compare two different measurement techniques.
Results
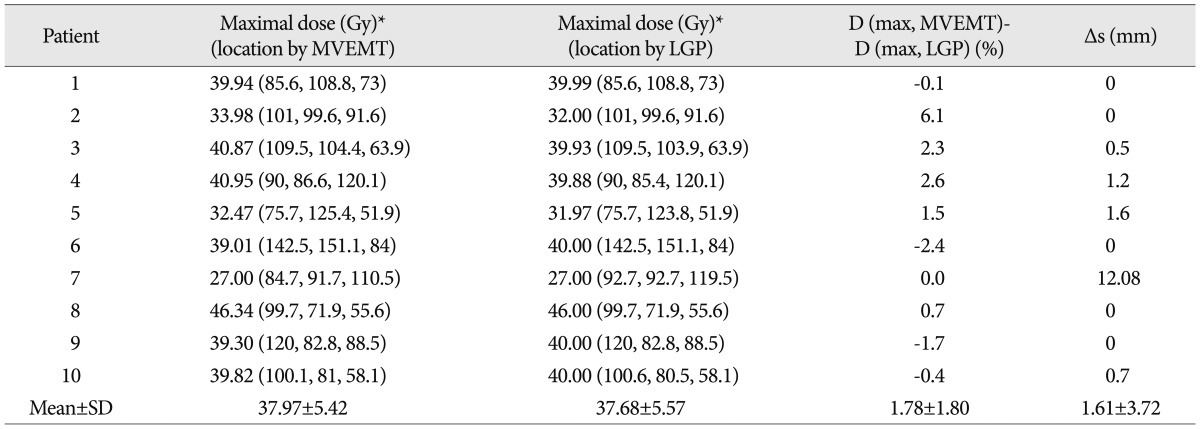
No statistical difference in dose at the 500 random points was observed between LGP and MVEMT. Differences in maximal dose ranged from -2.4% to 6.1%. An average distance of 1.6 mm between the maximal dose points was observed when comparing the two methods.
Conclusion
Statistical analyses demonstrated that MVEMT was in excellent agreement with LGP when planning for radiosurgery involving multiple target treatments. MVEMT is a useful, independent tool for planning multiple target treatment that provides statistically identical data to that produced by LGP. Findings from the present study indicate that MVEMT can be used as a reference dose verification system for multiple tumors.
INTRODUCTION
Leksell Gamma Knife® (LGK) system has been widely used to treat various brain diseases as a low-morbidity therapeutic modality1,2,4-6,12,13). Since, this is based on a single-fraction high dose treatment strategy, independent verification of the Leksell GammaPlan® (LGP) is important for ensuring patient safety and minimizing the risk of treatment errors10,13). Previous methods for verifying LGP by various algorithms were reported by Tsai et al.13), Marcu et al.11), Hur et al.9) and Zhang et al.14).
However, these verification methods were available only under a limited set of conditions. The method by Zhang et al.14)could calculate only treatment times, which were accurate only without plugs. Other methodologies only tested around the center of the target13). Additionally, these studies uniformly lacked statistical analysis. Instead of showing statistical agreement between their method and LGP findings, only the size of errors was reported11,13,14). Another significant limitation was that previous studies were tested exclusively on single treatment target. None of the previous studies showed accuracy for multiple targets. This means that findings from these previous investigations are not applicable to all LGK procedures, because a large portion of LGK treatment involves multiple targets.
In the present study, we have attempted to overcome these limitations. To do this, we determined for the first time whether a verification method could be applied in multiple target treatment accurately. Multiple target treatment refers to treatment plan for multiple brain lesions, such as multiple brain tumors.
Additionally, the accuracy of the verification method was validated by an expert in statistical analysis, which also was not tried so far.
MATERIALS AND METHODS
The modified variable ellipsoid modeling technique (MVEMT) was used as a verification method for our study9). For this, the patient's skull is viewed as an ellipsoid with the center at the mammillary body. The ellipsoid is expressed as following equation
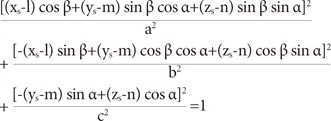
In which, (xs, ys, zs) are the coordinates of the shot center coordinate system (SCCS), (l, m, n) are the coordinates of the mammillary body in the SCCS and α=γ-90°, β is the angle rotated counterclockwise about the z's-axis of the skull. A single beamlet from the 201 collimators was defined as follows
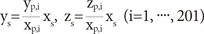
where (xp,i, yp,i, zp,i), (i=1,····, 201) are the geometrical locations of the 201 collimators in the SCCS. Dose rate for a single beamlet at the arbitrary point (p) is determined by the equation

in which, Ḋcal,18(0) is the calibration dose rate for the 18 mm collimator helmet, ωc is the collimator factor, di is the "i" beamlet depth, PWi is the plug weight (either 0 or 1), and F(ωc; ri) is the dose profile function related to dose distribution on the transverse plane of the beam axis. Therefore, the dose rate for one shot at point (p) is calculated with the formula
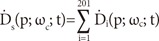
and, the dose at (p) from multiple shots (n) is expressed by the formula where ts (LGP) is the shot time calculated by LGP.
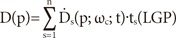
The equations were programmed using the hypertext preprocessor PHP scripting language (http://www.php.net). Calculation for all matrix points and the corresponding data were logged using MySQL® software (http://www.mysql.com) and later queried for necessary parameters. Starting in June 2010, we consecutively selected 10 patients with metastatic brain tumors with 2 to 4 targets. We treated all patients using an LGK stereotactic radiosurgery system.
Dose for 50 points in each patient
On the computer screen, we randomly selected 50 points for each patient, 40 within the target and 10 were out of the target. Those 50 coordinates of matrix along with the dose calculation at each point were assessed, by the LGP system. We then entered the same series of coordinates into the MVEMT program that calculated the dose at each location along with maximal dose (location) and target volume. All data were subsequently compared to the LGP results.
Maximal dose points
The maximal dose point refers to the point with the highest radiation dose for each round of Gamma Knife® treatment. We calculated the dose and dose rate at each of the 31×31×31 or 29791 point for one matrix. Dose rates were calculated while accounting for the contributions from the 201 beamlets. Since all multiple targets were irradiated with each treatment, the dose contribution from each shot was also included.
Target volume
When a new treatment is being planned, a three-dimensional conformal radiation therapy should be carefully designed which accurately conforms the isosurface of a given radiation dose to the anatomical boundaries of the tumor in its entire three-dimensional configuration. When the maximal dose is determined, the number of matrix points whose dose exceeded 50% of the maximal dose is queried in order to obtain the 50% dose volume. The target volume is defined as 50% dose volume.
Statistical analysis
To analyze the agreement of data produced by the two systems, LGP and MVEMT, a paired t-test was used (SPSS, version 12.0 : SPSS Inc., Chicago, IL, USA) : a p value of less than 0.05 was considered statistically significant. We also created a Bland-Altman plot to graphically compare the dose rates for 50 points as calculated by the two systems8). The Bland-Altman plot is constructed with the MedCalc software program (MedCalc®, Mariakerke, Belgium, http://www.medcalc.be/).
RESULTS
All pooled data included that from 500 points (50 points from each of the 10 patients). The average dose calculated by LGP showed 26.019±8.560 Gy, while the average dose calculated by MVEMT revealed 26.075±8.808 Gy.
Bland-Altman plots for all individual cases are shown in Fig. 1. For all 500 points, the mean difference between doses calculated by two methods, LGP and MVEMT, was -0.057 (95% CI) and standard deviation was 1.3353. The lower limit (2SD) of difference was -2.674 and the upper limit (2SD) of difference was 2.561. The case 6 revealed a mean difference of 0.692±2.542, deviation of data was much greater than the other cases, and had higher magnitude limit values (-4.290 for the lower limit and 5.674 for the upper limit). When we removed data for the case 6 from our analysis, better agreement between the two methods was observed in which the mean was -0.140 with a standard deviation of 1.0987, a lower limit (2SD) was -2.293 with a upper limit was 2.014 (Fig. 2). Table 1 shows results of the paired t-test performed to evaluate for the differences between the LGP and MVEMT for all 500 points. No statistical difference was observed.
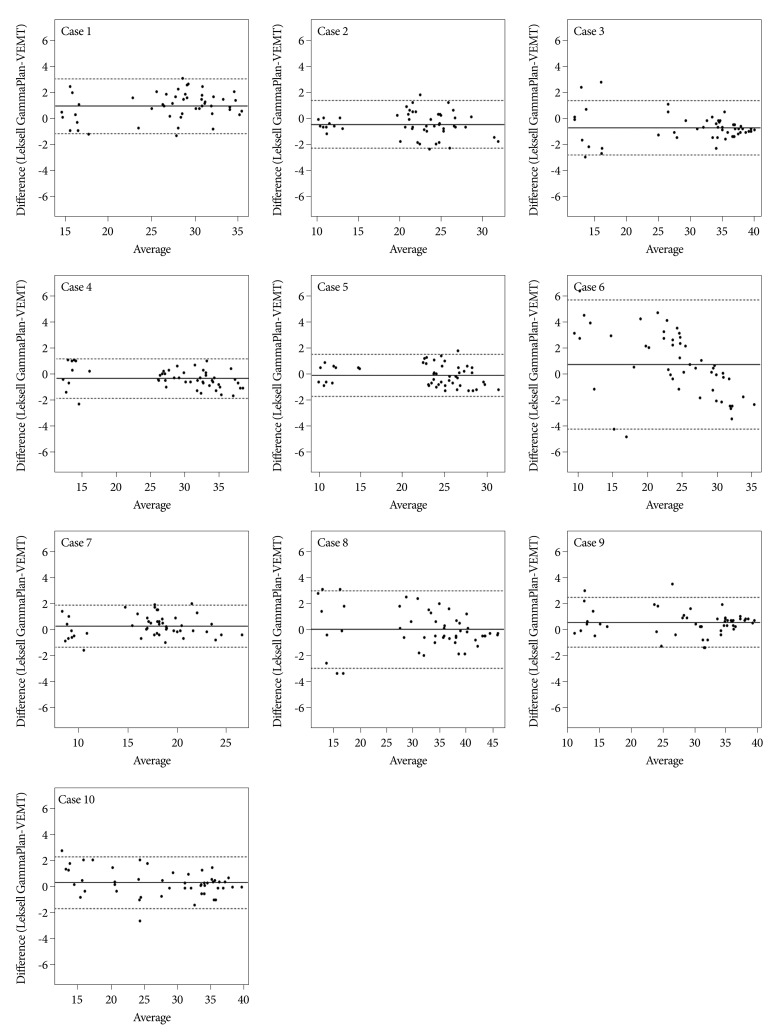
Bland-Altman Plots for each individual case. The middle line represents the mean difference between the LGP and MVEMT. The two extreme lines are the +1.96 and -1.96 standard deviations of the difference between the two methods. MVEMT : modified variable ellipsoid modeling technique, LGP : Leksell GammaPlan.
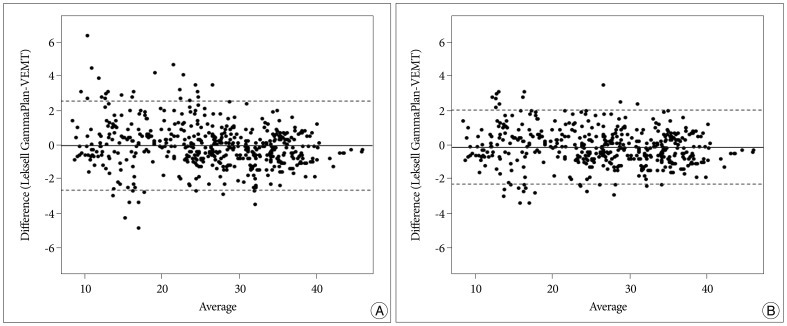
A : Bland-Altman Plot for all pooled data (n=500). The mean difference between doses calculated by two methods, LGP and MVEMT (95% CI) was -0.057. B : Bland-Altman Plot for data excluding case 6 (n=450). The mean difference between doses calculated by two methods (95% CI) was -0.140. The middle line is the mean difference between LGP and MVEMT. The two extreme lines are the +1.96 and -1.96 standard deviations of the difference between two methods. MVEMT : modified variable ellipsoid modeling technique, LGP : Leksell GammaPlan.
The maximal doses according to the MVEMT were averaged as 37.97±5.42 Gy, while that determined by the LGP was 37.68±5.57 Gy (Table 2). Differences in maximal doses ranged from -2.4% to 6.1% (Table 2). Close agreement was observed when comparing both methods with an average difference of maximal dose of 1.78±1.80%. Maximal dose points were identical for five cases including case 6 (Table 2). Data from case 7 showed largest distance (12.08 mm) between maximal dose locations determined by two methods. However, there was a 2.49% difference in the dose at the coordinate (84.7, 91.7, 110.5). The average of distance difference between maximal dose locations determined by two methods for entire cases was 1.61±3.72 mm (Table 2).
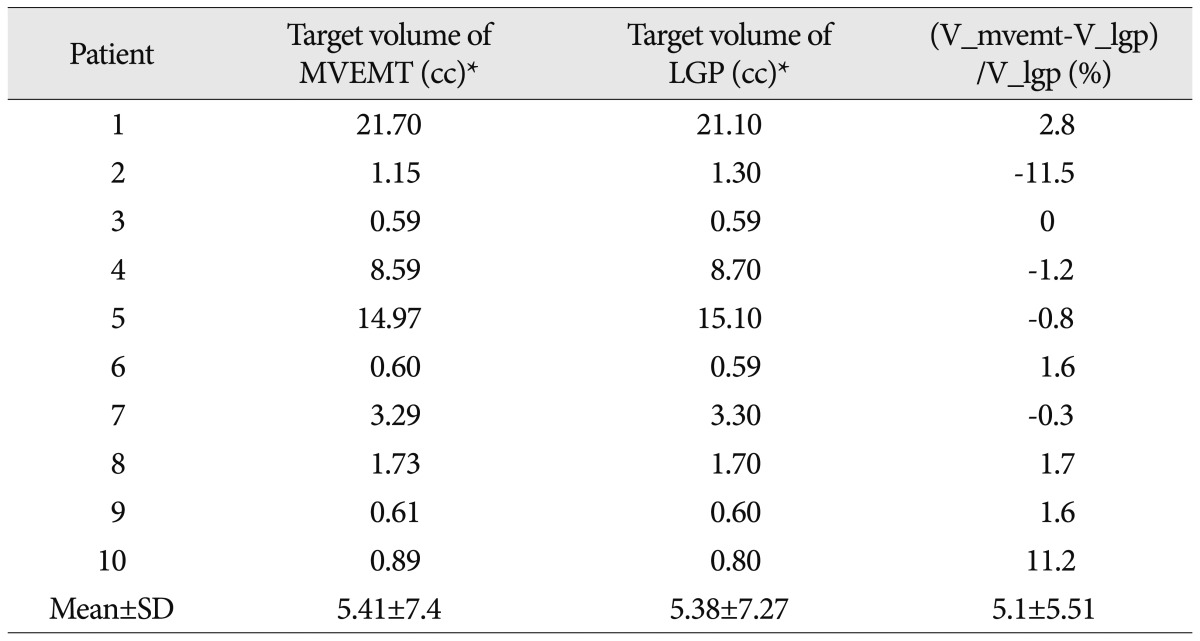
Target volumes ranged from 0.59 to 21.7 cc (5.41±7.40) according to MVEMT (Table 3). LGP showed that these volumes varied from 0.59 to 21.1 cc (5.38±7.27). The average volume calculated by the two methods differed by 5.1±5.51%. No statistically significant difference in target volume or maximal dose was observed.
DISCUSSION
The actual LGP algorithm is unknown. This may pose a challenge for designing an appropriate dose verification method for Gamma Knife® treatment. When a method is created, it would be far advantageous to obtain an algorithm with known formalism with secured agreement rate with LGP. In this regard, previous reports on verification methods are uniformly deficient due to a lack of statistical analysis9,11,13,14). Additionally, results of these studies were compared only in under certain conditions for limited parameters although many different LGP parameters are instantly available in clinical settings.
MVEMT is a method that simulates a patient's head as an ellipsoid. The biggest difference of MVEMT from other methods is parameters required for calculation are generated independently from LGP. For example, MVEMT measure the skull geometry from MRI, not from the bubble head measurement. Also, most previously developed methods require some parameters such as maximal dose point and skull measurements calculated by LGP.
Since independent verification methods adopt different calculation methods, implicit assumptions and approximations that produce errors under certain conditions are inevitable13). Thus, these modalities are not applicable to all matrix points. Tsai et al.13) applied average target depth from MRI images or ruler measurements. Since this group used a three-dimensional dose profile referred in unplugged condition, plugged treatments may produce errors depending on the numbers and location of plugs13). They explained that the discrepancies are due to the high dose gradient, especially when a plug pattern is used for the helmet. Their method revealed a 23.1% maximal dose rate mismatch for certain locations. Because this method produces errors in off-center points, it cannot be used for multiple targets. Marcu et al.11) used a constant radius R based on a spherical head. The accuracy of their method depended inversely on the deviation of the shape of a patient's head from a sphere. The method utilized by Zhang et al.14) adopted the tissue-maximum ratio for each of the 201 beams. Their method is related to accurately to the multiple-shot treatment plan because the accumulated error affects the normalization factor. Overall, the previous methods had limitations to be applicable for multiple targets.
However, a large portion of Gamma Knife® treatments involve multiple targets. In the authors' clinic, around 60% of all brain tumor cases consist of multiple targets, most of them were metastatic tumors. Previous report offered limited examples of verification of multiple shot treatments11). Only a few authors have reviewed results of multiple shot treatments. The method used by Marcu et al.11) had error ranges of 5% for a single shot and 3% for multiple shots, and did not provide a description of multiple targets. Zhang et al.14) neglected to mention whether or not their study was performed on multiple targets14). Multiple targets are subject to greater error because matrix points are more dispersed in the cranium. Minimum requirements for multiple target treatment are as follows : 1) a dose verification method with accuracy of off center points; 2) the ability to calculate the dose at all points in N matrices (N×31×31×31 points); 3) an off axis dose profiles complying with four collimator types; and 4) inherent error not multiplied over the number of targets. Unless any of these requirements are satisfied, dose verification cannot be performed accurately.
In our study, MVEMT showed excellent agreement with LGP according to the Bland-Altman analysis. This type of analysis is used to compare a measurement technique related to a reference value. The limit of agreement was considered to be two standard deviations within a range of 95% of the comparison points3). This method was more appropriate than correlation analysis when the reference method is low in error results7). LGP also exhibits inherent error when Gamma Knife® is used in an actual clinical setting. For example, bubble head measurements are subject to uncertainty due to orientation of the ruler against the surface of patients' head as well as the impact of existing scalp hair and its elasticity13). The aim of agreement analysis is to verify that two methods concur such that they can be used interchangeably.
According to the results of our study, MVEMT agrees sufficiently well with LGP. We selected random points from random matrices. The selected matrices were not chosen under certain constraints such as distance or shot numbers. In our investigation, 500 points were selected randomly from 297910 points (10×31×31×31) dispersed in the brain of 10 patients. These points statistically represented all arbitrary points in the skull regardless of shot numbers.
Some parameters showed greater variability. For example, target volumes had larger differences when comparing case 2 (11.5%), and case 10 (11.2%). The rate was exaggerated because it was measured in rate rather than the absolute difference in volume. The actual volume difference was 0.15 cc for case 2 and 0.09 cc for case 10. Even small differences in surface contour for each volume can create greater differences in rate. Additionally, Bland-Altman plots showed better results when case 6 was not included. It is not clear why this particular case was associated with worse agreement rate. However, both calculations had the exact same point (distance was 0) for the maximal dose point in case 6. Furthermore, the difference in maximal dose rate was 2.4% (Table 2) while the difference in target volume was 1.6% (Table 3). Since LGP and MVEMT generate numerous parameters, different range of agreement will be produced for each parameter. Some parameters will have greater agreement rate than others. This is why we compared more parameters for both systems than previous studies. Additionally, this also explains why statistical analysis is necessary when comparing two calculation methods.
When we consider the limitations of verification methods, MVEMT provided impressive results. The treatment design applied to all matrix points in this study was performed on multiple targets. Because MVEMT is based on single beamlet distribution, accurate calculation of dose rate can be performed regardless of collimator plugging. The results of this study indicate that accuracy of data from MVEMT is statistically sufficient for guiding any treatment design. To the best of our knowledge, this is the first report on clinical trial of dose verification for multiple target treatment with a statistical analysis. Further utilization of MVEMT is expected with comparison to newly designed verification methods.
CONCLUSION
In this study, the accuracy of MVEMT for evaluating multiple target treatments was compared to that of LGK. This method accurately verified important parameters of multiple target treatment design given by LGP, which was validated by statistical analysis. This ensures the quality of LGK treatment for multiple target cases. Further utilization of MVEMT as a reference verification method is expected for designing and/or comparing new verification methods.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (2010-0026432).